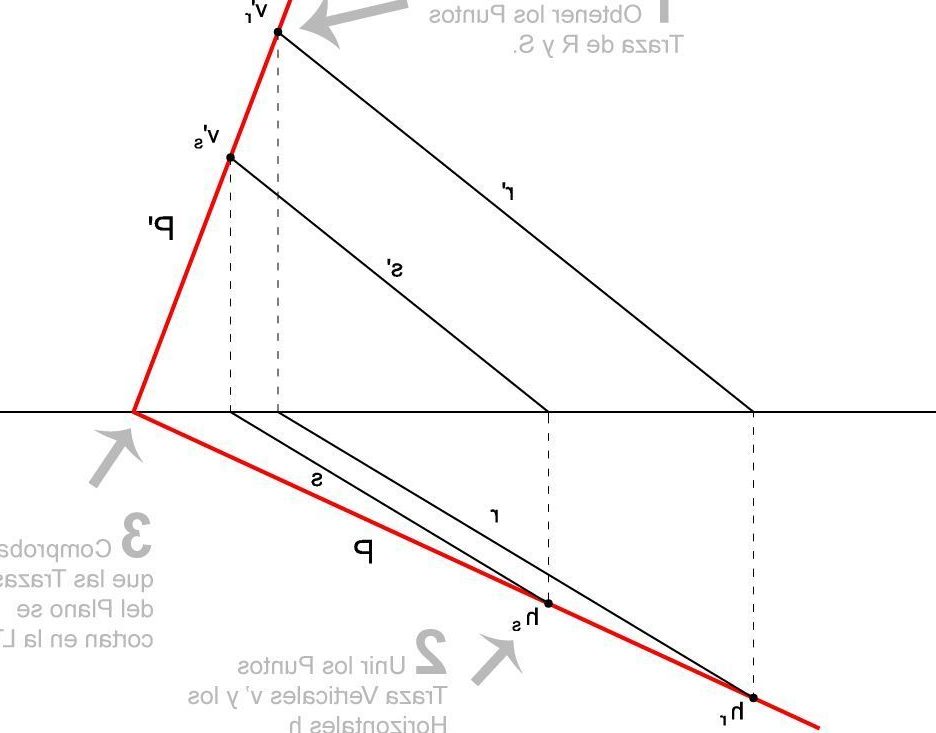
Proceso para definir un plano
En el sistema diédrico, la definición de un plano que pasa por 3 puntos puede realizarse siguiendo un conjunto de pasos específicos. Este proceso garantiza la correcta representación de un plano en el espacio tridimensional, tomando en consideración las proyecciones horizontales y verticales de los puntos involucrados. A continuación, se detallarán los pasos y consideraciones importantes para este procedimiento.
Pasos detallados
El proceso para definir un plano que pasa por 3 puntos diédrico es el siguiente:
- Se trazan las proyecciones horizontales y verticales de los puntos A, B y C.
- Se unen las proyecciones de los puntos dos a dos con segmentos de recta.
- Se halla el punto de intersección de las rectas que unen las proyecciones de los puntos.
- Se traza una recta perpendicular a la línea que une las proyecciones de A y B, que pase por el punto de intersección.
- La intersección de esta recta con el plano vertical de proyección determina la proyección horizontal del vector normal al plano que se busca.
- El plano se define por la proyección horizontal del vector normal y el punto de intersección de la recta perpendicular con el plano vertical.
Consideraciones importantes
Es importante considerar que en el proceso para definir un plano que pasa por 3 puntos diédrico, se deben respetar las normativas y convenciones del sistema diédrico. Además, la precisión en la representación de las proyecciones horizontales y verticales es fundamental para obtener un resultado certero.
Asimismo, la correcta aplicación de las operaciones y pasos mencionados es crucial para la obtención de la proyección horizontal del vector normal al plano y la definición precisa del plano en cuestión.